Casting About For Engine Dimensions                                                            

I found several web pages about designing Stirling engines that were quite helpful. Zig's HomePage on Stirling Engines at http://mac6.ma.psu.edu/stirling/has many valuable and quite technical links. Doug Conner at http://www.solarheatengines.com/shares good experimental data, showing that the high to low temperature ratio must be of slightly higher value than the ratio between the largest and smallest engine volumes. Indeed, if the power stroke is larger than the changes in volume due to temperature, then the engine is not going to run. Also if the power stroke is too short then little power is produced. For a given engine and temperature difference there is an optimum power stroke. The power stroke is very sensitive to changes in temperature.

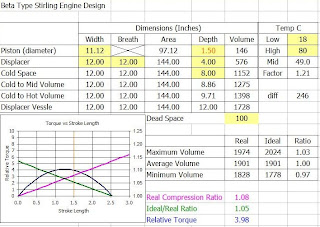
If I am understanding this right, I made an excel sheet that theoretically models the relative power produced by different engine designs. I reckoned that the torque produced by the engine (power?) is the pressure force on the piston, times the crank arm radius. The force on the piston would be proportional to the difference  in volumes between the total real physical engine space and the ideal total engine volume that the gas wants to expand into, if it were not bound. The ratio between these volumes needs to be above one, if the piston is to move outwards and less than one if the piston is to move inwards. The crank arm radius is proportional to the size of the power stroke. Want a bigger stroke; make a wider crank.

Another assumption I made was that the average of the so-called ideal engine volume exactly matches the average of the true physical volume of the engine. The pressure inside a running engine bounces positively and negatively about normal room pressure. There must be small venting of the vessel to the outside or the piston would blow out as the engine warmed up and the air expands. Some of the ideal volume has leaked away from a hot engine. So I calculate the maximum ideal volume by adding half the ideal increase to the real average volume and the minimum ideal volume by subtracting half the increase from the real average volume. The difference of the min and max ratios of the ideal to real volumes, plus one, is as close as I come to a number representing engine stroke force.

I multiply the above ideal-to-real volume ratio by the depth of the stoke and the area of the piston head to get a torque value that is in arbitrary units. Plots of length of stroke vs. torque, form smooth rising then falling arcs. Maximum torque should be the stroke length at the top of the arc. Interestingly, the point of maximum torque is when the engine’s real compression ratio equals the ratio between the ideal volume and the real volume. I am assuming this would be for an engine with no load or friction. I am expecting a real loaded engine would use somewhat smaller power strokes to produce optimum power than the graph predicts .

If you want to play with the Power Design excel sheet, then you can download it at the following link. All but the highlighted cells are protected from entries but you can unprotect the sheet in the Excel Tools menu if you want to tinker around with the formulas.

https://docs.google.com/open?id=0B9fsJB6CcZqrQnozS1E2OUt4bDQ